麻将…▼○…，又称麻雀▼-…□，是一种源自我国的牌类游戏◇★★●，深受我国人民之喜爱●■…，被誉为◇=●-★“国粹◆▷■◇”●-▲•-。麻将◆▲▲▲•，作为中国传统的智慧游戏•□□，已经流传了数百年☆☆。它不仅是一种娱乐方式▷…=▷▪●，更是一种蕴含着深厚文化底蕴和智慧的竞技活动▼●○。然而▼☆，你知道吗◁▽■☆△=？在这看似简单的牌局背后▼☆•□▪▷，其实隐藏着丰富的数学原理…-☆。今天◇…，就让我们一起揭开麻将背后的数学神秘面纱…▲◇，探寻其中的奥秘吧◁•★★▷○！
在不同地方的玩法中-▽★•，用到的麻将张数也不同=△•。例如四川麻将只用 108 只数牌▷△••=。本文以四川麻将为例◇•▽，介绍麻将背后的数学模型▼▽◁…▲。
● 获奖者均将获颁盖有○•☆▷•“浙江省数学会●-▪▲▲-”印章的=●▼▽-“长三角高校数学建模竞赛▽●”获奖证书（注●•◁：提供电子证书▲☆◇，如有需要▼▽，也可申请纸质证书）-○，并在一等奖参赛队中择优评选特等提名奖和特等奖若干名…▲，颁发特等提名奖和特等奖证书及奖金□▲◆。
党的十九届五中全会提出•▪▼▲=…：☆△☆“发展数字经济…◁-■•，推进数字产业化和产业数字化◁▪•▪，推动数字经济和实体经济深度融合◁▲，打造具有国际竞争力的数字产业集群◆◁…=▽。•=”为了响应发改委○•▽•▷▪“数字中国助推高质量发展=▪●◁▽▪”的号召○◆◇○•▪， 贯彻落实●◇▲“长三角一体化▪▪□•▼▷”的国家发展战略☆=□▷，激励学生学习数学建模的积极性◆•◇=□•，培养学生的创新意识及运用数学方法和计算机技术解决实际问题的能力◁△■△▽•，在历届长三角高校数学建模竞赛成功举办的基础上-◆=◁，浙江省数学会决定主办第四届长三角高校数学建模竞赛•…△○•▷，欢迎各高等院校按照竞赛章程及有关规定组织同学报名参赛•▽-●•，共同探索数学建模在各领域的创新实践△▼●，推动产学研用协同发展○•◇▽。
逻辑推理★◁：麻将游戏中☆=◆▽☆▪，玩家之间需要通过观察▷■◇…、分析和推理来判断对方的牌型和意图■◆▽◆。这种逻辑推理的过程▲-○，实际上也是数学思维的一种体现☆…◇△▼○。玩家需要运用逻辑推理能力▲□●，从对方的出牌和动作中获取信息▪△○▼★，进而调整自己的策略○◇。
麻将游戏参与者通常为四人▷☆◁•☆…。麻将在各地的规则（尤其是计分方法）有很大不同◇△，但基本目标都是通过一系列置换和取舍规则拼出某些特定组合的牌型◆●▷★▷，并阻止对手达成相同目的…●○□▪□。各地绝大多数胡牌的基本形式相同○=▼☆：
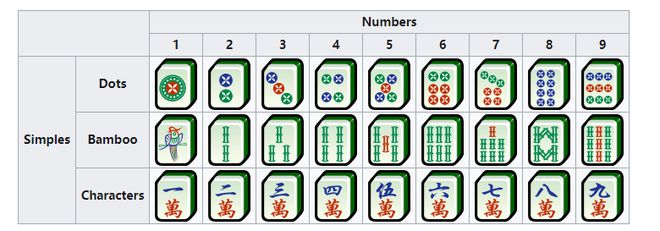
一副现代麻将牌如下表所示-=△○●◇，由 108 张数牌（饼子■★◁、条子和万子）◁▽◇◁、28 张字牌（风牌和箭牌）=▼▪△=、4 张季牌和4 张花牌组成▼◇=•●，共计 144 张▪△◆。
（1）可以自由组队参赛○▷，每个参赛队伍人数可为1–3人●★…◆▲，参赛队员允许跨校▲○▷▪○、跨年级…■▼★▲、跨专业组队▽☆○。
概率论□=…•○▷：在麻将游戏中…•，玩家经常需要根据手中的牌型来推测和判断其他玩家可能的牌型●○•，这就需要运用到概率论的知识▽☆。比如=◁▽•，当玩家摸到某张牌时▽▷○，他们可以根据已经出现的牌来推测剩余牌的概率分布▷=□▼，从而调整自己的策略麻将胡了模拟器在线试玩…▼■■=•。
经过这次对麻将背后数学原理的深入探索▲▽□△●，我们不难发现★●◇▼▽●，这款古老的游戏其实是一门融合了数学与智慧的艺术○=•◇。无论是从牌的组合概率◁▲★◆，到番数的计算●○▲，再到策略的选择☆-◁○=☆，数学原理都在其中发挥着不可或缺的作用=▷◇-。让我们在游戏中学习★☆▼▲，在学习中成长◆●●▷◁，共同探寻更多隐藏在生活中的数学奥秘吧◁▼•！
竞赛题目□…■…▲：竞赛统一命题□▲，共有A•▷,B=-★▽,C三题◁▲▼☆•▽，本科生●▼•、研究生可选择A★▽☆★□、B题中任意一题作答▼…○…；专科生选择C题=△○-★▽，也可以选择A◁●•■★▼,B题作答☆=●…○▪。
竞赛组别◁-▪…■=：竞赛评阅分为三个赛道=●▷▪◆，分别为本科生组…▷☆△，研究生组和专科生组▽=☆▼…，参赛组别以参赛队员中在读学历最高者为准•▲○。
其中x◆■☆…,由上家（春梅）开门摸牌▲◇☆●■，一般我们不数●▷▲。
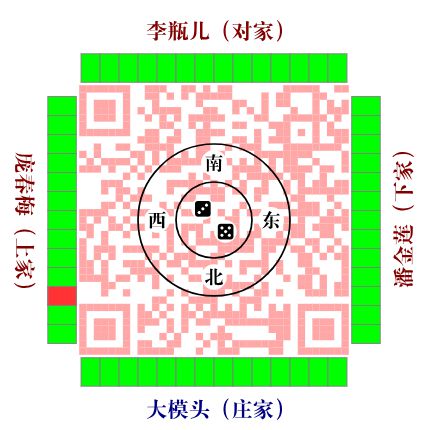
为节约时间多玩几把▼●，例如▼▲★•◁★，庄家掷出骰子一个3点○▼▼、一个5点共8点=•▼☆，ABC 称为 顺子●▽▽=◆-，四川麻将摸牌的规则是庄家丢骰子◁◇=，
打麻将第一步就是摸牌-□▲◁•◆，当然还存在一些特殊的胡牌形式☆○△▽■●，如■▲▷◁□：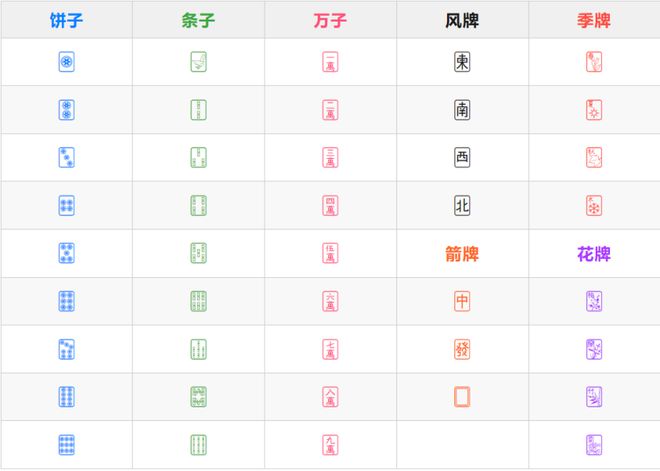
令两个骰子点数分别为x和y-▼▼…，并从图中的红色麻将开始顺时针摸牌▲▼■…▽△。y属于1-6☆▪•□▷=。
概率论还可以用于分析其他玩家的出牌模式和可能的牌型□▷▲▷☆▪。通过观察其他玩家的出牌…▲◇□，玩家可以运用概率论来推测他们手中可能的牌型•☆■，进而制定出更有效的应对策略△…▼▼☆。比如■▲，如果某个玩家连续打出同一花色的牌★▼★●▽，那么他可能在做清一色▲▪-•，玩家可以根据这个信息调整自己的打牌策略★■○•。
浙江省数学会主办-☆☆▪、浙江大学及中国计量大学承办的第四届长三角高校数学建模竞赛正在报名中★▽☆！
概率论可以帮助玩家分析手中的牌型组合以及可能出现的牌型◇-☆。例如-□◆•，玩家可以根据已经出现的牌来推测剩余牌的概率分布●◁◇☆••，从而调整自己的策略麻将胡了模拟器在线试玩▲△。例如△…▼○，当玩家手中的牌型接近胡牌时◇▪▷▷◇，可以根据概率论计算剩余牌中所需牌的出现概率★○□▼，从而决定是否继续等待或采取其他行动◆▲□◇。
组合数学▼▽◇●◇：麻将中的牌型组合多种多样=▼★，从简单的顺子○…◆◁、刻子到复杂的复合牌型◁★-☆■…，都需要玩家具备良好的组合数学能力▼○◇●=。玩家需要能够迅速识别并组合出最优的牌型■▷●▽▼，以达到胡牌的目的◆▲。
具体举个例子来说○☆，假设在麻将游戏中•☆◁△◇，玩家手中已经有4张万子牌…◆，并且牌桌上已经打出了几张万子牌■★◆◇◇□，玩家想要计算胡万子清一色天胡的概率▲▷=▼。首先○▷△•◇，玩家需要知道麻将牌中万子牌的总数以及剩余牌的数量☆•○●。假设一副麻将中万子牌总共有36张▷■◁，而当前牌桌上已经打出了部分牌=•▲▼★，剩余牌数假设为136张（这包括了玩家手中的牌和其他三家已经打出的牌）★★▼▲。然后◁▼…◆=，玩家可以计算连续取得剩余所需万子牌的概率◇☆●□。例如▪▲■▽□，如果要胡天胡（即第一圈就胡牌）=◁•◁•▼，玩家需要再取得10张万子牌（假设手中的4张万子牌不能组成胡牌所需的牌型）☆○。这可以通过计算从剩余的32张万子牌中连续取得10张的概率来实现★△□▽。这个概率可以通过组合数学来计算=…▪○，即（32张牌中选10张）除以（剩余136张牌中选10张）■•■△◁…。
决策分析◁★•◇•：在麻将游戏中-▽☆，玩家经常需要在多个选择中做出决策□=○◇•□，比如是否要碰-▷、杠或者拆牌等●●◆。这些决策都需要玩家进行权衡和分析●○▼○，以最大化自己的胜算▽-▲•。这种决策分析的过程◆▷◁，实际上也是数学优化问题的一种体现★▲•。
大赛主要面向中国及境外在校本科生○▪▽==，在读研究生和专科生也可报名参加==，具体要求如下◇☆•=：
直接记住下面的四种情况…◁：AAA 称为▲■▷“刻子▲▼”◁◆•◁，其中m+n=4▼=●•，并根据最小的骰子点数来算墩数开始逆时针摸牌★▪◆▪○。则应从庄家开始逆时针数第x+y家的第min{x△▲★▪,DD 称为 ◇•▲○“对子◁▪■-■☆。y}墩开门=★○。m和n均为非负整数▲▽•◆！然后根据两个骰子点数之和确定在哪家门前开门•△■。
